Definir correlación de series de tiempo
El comando 'Definir correlación de series de tiempo' hará que dos o más series de tiempo ya no sean completamente independientes entre sí, sino que se guíen por una matriz de correlación.
Al igual que las correlaciones de las distribuciones de @RISK, las correlaciones de series de tiempo añaden la función de propiedad RiskCorrmat a las funciones de series de tiempo. Por ejemplo, la siguiente función de serie de tiempo:
{=RiskAR1(0,0.05,0.25,0)}
Se actualiza de la siguiente manera cuando se añade a una matriz de correlación llamada "MiCorrelacion":
{=RiskAR1(0,0.05,0.25,0,RiskCorrmat(MiCorrelacion,1))}
Especificación de las entradas
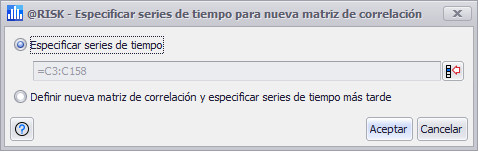
Figura 1 - Especificar series de tiempo
Al crear una nueva matriz de correlación para una serie de tiempo, la primera ventana que se abre es la de Especificar serie de tiempo que incluye dos opciones:
Una vez especificadas las entradas, se abrirá la ventana Definir correlación. Para mayor información, consulte la ventana Definir correlación.
Comprensión de la correlación de series de tiempo
Es importante entender que las correlaciones entre series de tiempo son fundamentalmente diferentes de las que existen entre distribuciones estándar. Una correlación entre dos funciones de series de tiempo indica que en cada iteración el conjunto de valores devueltos por las dos series de tiempo está sujeto al coeficiente de correlación especificado. En cambio, la correlación entre dos funciones de probabilidad estándar de @RISK requiere toda la simulación para que esa correlación sea evidente.
Para entender cómo se implementa la correlación de @RISK, es importante darse cuenta de que los modelos de series de tiempo generan el valor en un momento determinado basándose en uno o más valores conocidos de períodos de tiempo anteriores más un término de ruido distribuido aleatoriamente. Son las distribuciones de ruido las que obedecen a las correlaciones que se especifican.
También tenga en cuenta que las correlaciones especificadas siempre se aplican al modelo de series de tiempo estacionarias subyacentes antes de aplicar cualquier transformación (como la exponenciación o la integración). Una forma común de generar series de tiempo correlacionadas es utilizando el comando de ajuste por lotes, que como parte de su salida construye una matriz de correlación. Los coeficientes en esa matriz serán las correlaciones entre los datos después de que se hayan aplicado todas las transformaciones de datos especificadas a cada una de las series. Por ejemplo, imagine que hay dos series de datos que son precios de acciones. Es muy habitual utilizar una transformación logarítmica y una primera diferenciación para convertir los valores brutos en rendimientos del período antes de ajustarlos. Son estos rendimientos, y no las series de datos en bruto, para los que se calculan los coeficientes de correlación.
Algunas funciones de series de tiempo, los llamados modelos regresivos, tienen un estado de equilibrio al que la serie se ve fuertemente arrastrada si se producen desviaciones apreciables de ese equilibrio. Si dos series de tiempo están correlacionadas y una o ambas están fuera de equilibrio al comienzo de las series, cualquier correlación especificada entre ellas puede verse abrumada al comienzo de la previsión por la necesidad de que la serie vuelva a su estado de equilibrio. A menudo, las correlaciones deseadas sólo se consiguen después de un periodo de "rodaje" en el que las series vuelven a estar en equilibrio. (Por cierto, esto también significa que las correlaciones para la serie temporal BMMRJD sólo serán aproximadas, ya que cada vez que se produzca un salto, su necesidad de recuperarse de ese salto superará el efecto de las correlaciones).