RiskDiscrete
|
Description |
RiskDiscrete({X1,X2,...,Xn},{p1,p2,...,pn}) specifies a general discrete distribution with n possible outcomes. Each possible outcome has a value X and a probability weight p that specifies the outcome's likelihood of occurrence. The probability weights can sum to any value, but internally, @RISK normalizes them so that they sum to 1. This distribution is very flexible and can be used for any discrete set of possibilities.
|
|
Examples
|
RiskDiscrete({0,5},{1,1}) returns a discrete distribution with two equally probable values, 0 and 5. Although the weights are 1 and 1, @RISK will normalize them to probabilities, 0.5 and 0.5. RiskDiscrete(A1:C1,A2:C2) returns a discrete distribution with three possible outcomes. Cells A1 through C1 hold the possible values, and cells A2 through C2 hold the probability weights.
|
|
Guidelines |
The probability weights must be nonnegative. |
|
Parameters |
{x} = {x1, x2, ..., xN} array of continuous parameters {p} = {p1, p2, ..., pN} array of continuous parameters
|
|
Domain |
discrete
|
|
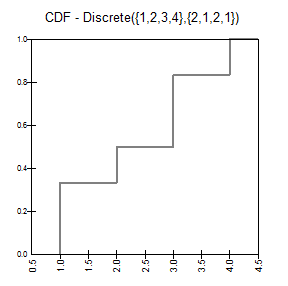
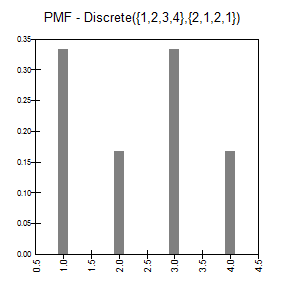
Mass and Cumulative Distribution Functions |
The arrays are assumed to be ordered from left to right. The p array is assumed to be normalized so that they sum to 1.
|
|
Mean |
|
|
Variance |
|
|
Skewness |
|
|
Kurtosis |
|
|
Mode |
The x-value corresponding to the highest p-value. |
|
Examples |
|