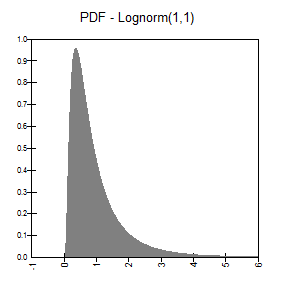
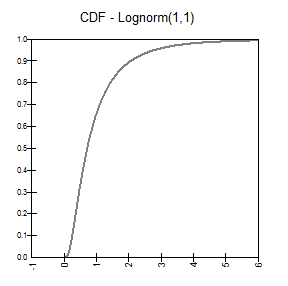
RiskLognorm

Descripción

RiskLognorm(media, desviación estándar) especifica una distribución lognormal con los valores asignados de media y desviación estándar. Los argumentos de esta forma de distribución log-normal especifican la media y desviación estándar de la distribución log-normal de probabilidad generada.

Igual que la distribución Normal, la LogNormal posee dos parámetros ( (μ,σ) correspondientes a la media y a la desviación estándar. De la misma forma que la distribución normal resulta de añadir muchos procesos aleatorios, así también la Lognormal resulta de la multiplicación de muchos procesos aleatorios. Desde un punto de vista técnico, esta es una extensión directa de los resultados previos ya que el logaritmo del producto de números aleatorios es igual a la suma de los logaritmos. En la práctica, es frecuentemente utilizada como una representación del valor futuro de un activo cuyo valor en términos porcentuales cambia de una forma aleatoria e independiente. Es frecuentemente utilizada en la industria del petróleo para modelar reservas posterior a los estudios geológicos cuyos resultados sean inciertos. La distribución posee una seria de propiedades deseables respecto de proceso del mundo real. Estas incluyen el hecho de que sea sesgada positivamente y de que pose un rango positivo y no acotado, es decir, tiene un rango desde 0 al infinito. Otra propiedad útil es el hecho que cuando σ es pequeño con respecto a μ, el sesgo es pequeño y la distribución tiene a una distribución Normal, de forma tal que una distribución Normal puede ser aproximada por medio de una LogNormal utilizando la misma desviación estándar, pero incrementando la Media (de forma tal que la razón σ / μ sea pequeña), y luego desplazando la distribución al añadir una cantidad constante de forma tal que sus Medias coincidan.

Ejemplos

RiskLognorm(10,20) especifica una distribución log-normal con una media de 10 y una desviación estándar de 20.

RiskLognorm(C10*3.14,B10) especifica una distribución log-normal con una media igual al valor de la celda C10 multiplicado por 3,14 y una desviación estándar igual al valor de la celda B10.

Reglas

La media y la desviación estándar deben ser mayor que 0.

Parámetros

     parámetro continuo      

     parámetro continuo      

Dominio

     continuo

Funciones de distribución de densidad y acumulativa

con

y

Donde, es la función de distribución acumulada de una Normal(0,1) también denominada Integral de Laplace-Gauss.

Media

Varianza

Índice de sesgo

Curtosis

con

Moda

Ejemplos