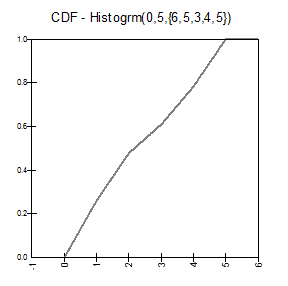
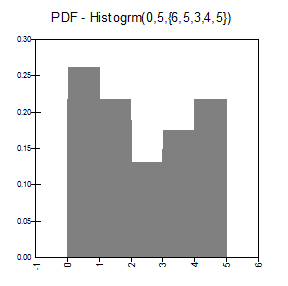
RiskHistogrm
|
Descripción |
RiskHistogrm(mínimo, máximo, {p1,p2,...,pn}) especifica una distribución de histograma definida por el usuario con un rango definido por los valores mínimo y máximo. Este rango se divide en n clases. Cada una de las clases tiene un coeficiente de probabilidad p que refleja la probabilidad de que ocurra un valor en esa clase. Estos coeficientes de probabilidad pueden adoptar cualquier valor, el único factor importante es el coeficiente de probabilidad de una clase con respecto a otra. Esto quiere decir que la suma de todos los coeficientes de probabilidad no tienen que ser igual a 100%. @RISK normalizará las probabilidades de las diferentes clases. La normalización de estos coeficientes se lleva a cabo sumando todos los coeficientes de probabilidad y dividiendo cada uno de ellos por el total de la suma.
|
|
Ejemplos |
RiskHistogrm(10,20,{1,2,3,2,1}) especifica un histograma con un valor mínimo de 10 y uno máximo de 20. Este rango se divide en 5 clases de igual longitud ya que hay 5 valores de probabilidad. Los coeficientes de probabilidad de las cinco clases son los argumentos 1, 2, 3, 2 y 1. Las probabilidades que se corresponderán con estos coeficientes serán 11,1% (1/9), 22,2% (2/9), 33,3% (3/9), 22,2% (2/9) y 11,1% (1/9). Estos valores se normalizan dividiéndose entre 9 para que la suma de todos ellos sea igual al 100%. RiskHistogrm(A1,A2,B1:B3) especifica un histograma con un valor mínimo tomado de la celda A1 y uno máximo tomado de la celda A2. Este rango se divide en 3 clases de longitudes iguales ya que hay 3 valores de probabilidad. Los coeficientes de probabilidad se toman de las celdas B1 a B3.
|
|
Reglas |
Los valores de los coeficiente representados por p deben ser mayores o iguales a cero, y la suma de todos los coeficientes debe ser mayor que cero. |
|
Parámetros |
min parámetro continuo min < max * max parámetro continuo {p} = {p1, p2, ..., pN} arreglo de parámetros continuos,
*min = max se soporta para la conveniencia en la creación de modelos, pero devendrá en una distribución degenerada.
|
|
Dominio |
|
|
Funciones de distribución de densidad y acumulativa |
En donde el arreglo {p} ha sido normalizado para generar un histograma de área unitaria. |
|
Media |
No posee forma cerrada
|
|
Varianza |
No posee forma cerrada
|
|
Índice de sesgo |
No posee forma cerrada
|
|
Curtosis |
No posee forma cerrada
|
|
Moda |
No definido de forma única
|
|
Ejemplos |
|