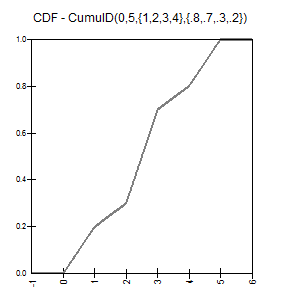
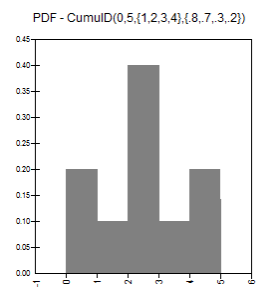
RiskCumulD
|
Descripción |
RiskCumulD
|
|
Ejemplos |
RiskCumulD(0,10,{1,5,9},{0.9,0.3,0.1}) especifica una curva acumulativa con tres datos de puntos y un rango de 0 a 10. El primer punto de la curva es 1 con una probabilidad acumulativa descendente de 0,9 (10% de los valores de la distribución son menores o iguales a 1 y el 90% son mayores). El segundo punto de la curva es 5 con una probabilidad acumulativa descendente de 0,3 (70% de los valores de distribución son menores o iguales a 5 y el 30% son mayores). El tercer punto de la curva es 9 con una probabilidad acumulativa descendente de 0,1 (90% de los valores de distribución son menores o iguales a 9 y el 10% son mayores). RiskCumulD(100,200,A1:C1,A2:C2) especifica una distribución acumulativa con tres datos de puntos y un rango de 100 a 200. La fila 1 de la hoja de cálculo —de A1 hasta C1— contiene los valores de cada dato de punto, mientras que la fila 2 —de A2 hasta C2— contiene la probabilidad acumulativa de cada uno de los 3 puntos de la distribución. En Excel no es necesario utilizar llaves cuando se utilizan rangos de celdas como entradas de una función.
|
|
Reglas |
Los puntos de la curva deben especificarse en orden ascendente de valores (X1 < X2 < ... < Xn). Las probabilidades acumulativas p de los puntos de la curva deben especificarse en orden descendente de probabilidades acumulativas descendentes (p1 >= p2 >= ... >= pn). El mínimo debe ser menor que el máximo. El mínimo debe ser menor que X1 y el máximo debe ser mayor que Xn. El número máximo de pares X,p es 2.147.483.647. |
|
Parámetros |
min parámetro continuo min < max max parámetro continuo {x} = {x1, x2, ..., xN} arreglo de parámetros continuos {p} = {p1, p2, ..., pN} arreglo de parámetros continuos |
|
Dominio |
|
|
Funciones de distribución de densidad y acumulativa |
Los arreglos están ordenados desde izquierda a derecha El índice i va desde 0 hasta N+1, con dos elementos extra:
|
|
Media |
No posee forma cerrada
|
|
Varianza |
No posee forma cerrada
|
|
Índice de sesgo |
No posee forma cerrada
|
|
Curtosis |
No posee forma cerrada
|
|
Moda |
No posee forma cerrada
|
|
Ejemplos |
|