Agrupamiento Chi-Cuadrado
La prueba Chi-cuadrado es un método para determinar la "bondad de ajuste" de una distribución estimada; la prueba Chi-cuadrado es una alternativa a las pruebas Kolmogorov-Smirnov (K-S) y Anderson-Darling (A-D). Todas estas estadísticas se utilizan para analizar la calidad de un ajuste. Sin embargo, a diferencia de las pruebas K-S y A-D, la prueba de Chi-cuadrado depende de la clasificación de los datos, por lo que es fundamental una categorización adecuada.
Si no está seguro del número de intervalos para el conjunto de datos, elija 'Auto' para el 'Número de intervalos' y establezca el 'Arreglo de intervalos' en 'Probabilidades iguales'.
Configuración 'Agrupamiento Chi-Cuadrado'
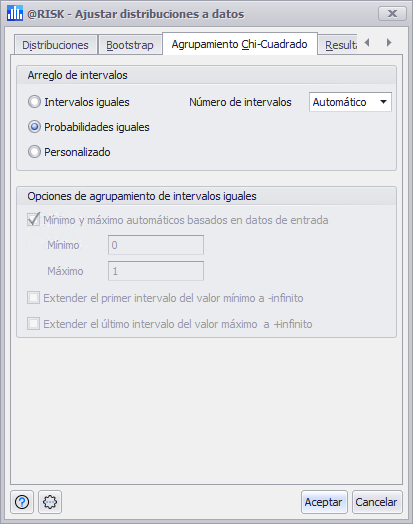
Figura 1 - Ajustar distribuciones datos - Pestaña 'Agrupamiento Chi-cuadrado'
La pestaña 'Agrupamiento Chi-cuadrado' de la ventana 'Ajustar distribuciones a datos' (Figura 1, derecha) incluye las opciones de configuración para las pruebas Chi-cuadrado que se ejecutan durante el proceso de ajuste. La pestaña incluye dos secciones:
Arreglo de intervalos
El Arreglo de intervalos determina cómo se clasificarán los valores de los datos para la prueba de Chi-cuadrado; los valores del conjunto de datos se pueden clasificar en las siguientes maneras:
El 'Número de intervalos' tiene por defecto el valor 'Auto'; para introducir un valor diferente, haga doble clic en el campo y escriba el número de intervalos que deben utilizarse en la prueba.
Opciones de agrupamiento a intervalos iguales
Si se elige 'Intervalos iguales' para la disposición de los recipientes, esta sección se activa. Cualquiera (o todas) de las siguientes opciones pueden ser establecidas para configurar los contenedores de intervalos iguales:
Tanto si está marcada la opción 'Mínimo y máximo automáticos basados en datos de entrada' como si se fijan manualmente los valores mínimo y máximo, el primer y el último intervalo se seguirán configurando de acuerdo con las opciones establecidas para los ajustes 'Extender el primer intervalo del valor mínimo hasta -infinito' y 'Extender el último intervalo del valor máximo hasta +infinito'.
Intervalos personalizados
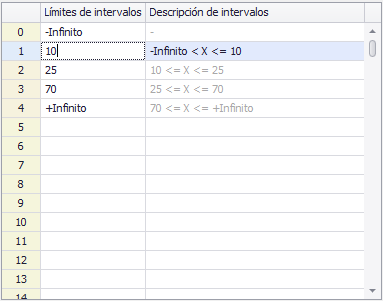
Figura 2 - Intervalos personalizados
En situaciones en las que los intervalos deben tener longitudes desiguales (es decir, cuando existen agrupaciones naturales), se pueden configurar intervalos personalizados (Figura 2, derecha). Al configurar el primer intervalo, introduzca el valor inicial de ese intervalo; para cada intervalo posterior, introduzca el valor final. A medida que se introducen los valores en los campos de los límites de los intervalos, la descripción de los intervalos se completará con la fórmula lógica de ese intervalo.
De forma similar a los grupos de igual tamaño, el primero y el último intervalo pueden configurarse para que se extiendan hasta menos y más infinito cuando se trabaja con un conjunto de datos con límites desconocidos. Por ejemplo, la figura 2 ilustra una configuración de intervalos en la que el primer intervalo se extiende desde "menos infinito hasta menos de 10", y el último intervalo se extiende desde "mayor o igual a 70 hasta más infinito".