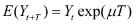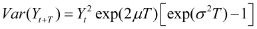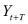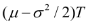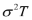RiskGBM
|
Description
|
RiskGBM A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the series follows a Brownian motion, also called a Wiener process. In a financial context, the series is typically the price of a security, which is lognormally distributed. In this case, the “log return” of the series, essentially the change in the price, is normally distributed. The RiskGBM function requires an exponential transformation and first order integrations. This is done by using the RiskTSTransform and RiskTSIntegrate property functions.
|
|
Examples
|
RiskGBM(0.01, 0.05, RiskTSTransform(1,0), RiskTSIntegrate(1,1)) generates a GBM process with drift 1% and volatility 5%. RiskGBM(C10, C11, RiskTSTransform(1,0), RiskTSIntegrate(1,1)) generates a GBM process with parameters taken from cells C10 and C11.
|
|
Technical Details |
Define Then for any
The discrete equivalent of this is
The conditional mean and variance of
and
If this is in a financial context and |
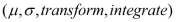
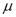
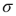
 = a sample from a Normal(0,1) distribution
= a sample from a Normal(0,1) distribution ,
, 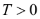 ,
,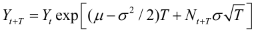


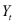 ,
,